Skip to main content

材料

可通入如下三种方式进入材料设置窗口：

  • 在工具菜单下选择材料，进入材料设置窗口
  • 点击工具栏中的材料按钮，进入材料设置窗口
  • 点击模型树中材料右侧的加号+，进入材料设置窗口

选择已有的材料或新增材料并设置对应的参数，自定义材料参数设置好后点击保存按钮可保存至个人材料库，点击应用按钮可应用至当前模型。

20220706173938

本构模型​

目前Mslope支持Mohr-Coulomb以及Drucker-Prager两种材料模型，这两种本构模型的屈服面在主应力空间(σ1−σ2−σ3)(\sigma_1-\sigma_2-\sigma_3)中的几何形状如下所示。

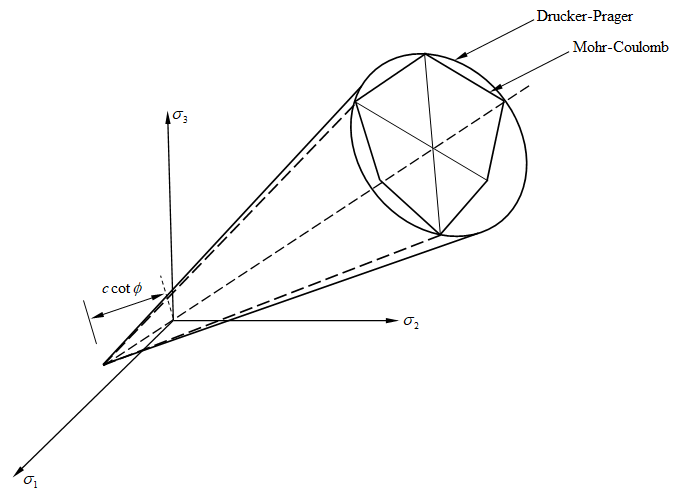
20220708141056

Mohr-Coulomb本构模型​

Mohr-Coulomb 塑性本构模型主要适用于在单调载荷下的颗粒状材料，在岩土工程中应用非常广泛。

屈服面​

Mohr-Coulomb模型屈服面函数为

F=psin⁡ϕ+σˉ(cos⁡θ−13sin⁡ϕsin⁡θ)−ccos⁡ϕ=0F=p\sin{\phi}+\bar{\sigma}(\cos{\theta}-\frac{1}{\sqrt{3}}\sin{\phi}\sin{\theta})-c\cos{\phi}=0

其中c(κ)c(\kappa)和ϕ(κ)\phi(\kappa)分别为粘聚力和内摩擦角，其与硬化参数κ\kappa有关，θ\theta为应力洛德(Lode)角，p=I1/3p=I_{1}/3，I1I_{1}为第一应力不变量。

塑性势面​

Mohr-Coulomb屈服面存在尖角，如采用相关联的流动法则（即塑性势面与屈服面相同），将会在尖角处出现塑性流动方向不是唯一的现象，导致数值计算的繁琐、收敛缓慢。为了避免这些问题，这里采用对尖角进行特殊处理取值，以保证计算的收敛性。为了更准确地计算剪胀性，塑性势面与屈服面不同，但也具有类似的结构。

G=psin⁡ψ+σˉ(cos⁡θ−13sin⁡ψsin⁡θ)−ccos⁡ψ=0G=p\sin{\psi}+\bar{\sigma}(\cos{\theta}-\frac{1}{\sqrt{3}}\sin{\psi}\sin{\theta})-c\cos{\psi}=0

这里ψ\psi为剪胀角。

硬化规律​

Mohr-Coulomb模型可以考虑屈服面大小的变化，通过控制硬化参数κ\kappa线性改变屈服面的大小，从而控制屈服面的硬化规律。

Drucker-Prager本构模型​

屈服面​

Drucker-Prager模型屈服面函数为

F=3α′(κ)p+σˉ−K(κ)=0F=3\alpha^{'}(\kappa)p+\bar{\sigma}-K(\kappa)=0

其中

α′=2sin⁡ϕ3(3−sin⁡ϕ),K=6cos⁡ϕ3(3−sin⁡ϕ)\alpha^{'}=\frac{2\sin{\phi}}{\sqrt{3}(3-\sin{\phi})},K=\frac{6\cos{\phi}}{\sqrt{3}(3-\sin{\phi})}

塑性势面​

与屈服面类似，将屈服面中的内摩擦角ϕ\phi替换为剪胀角ψ\psi。

硬化规律​

同Mohr-Coulomb模型。

材料参数​

一般​

  • 排水类型：默认为排水状态的参数，暂不可更改。
  • 容重：材料单位体积所具有的重量。

弹性​

  • 弹性模量：有力施加于物体或物质时，其弹性变形（非永久变形）趋势的数学描述。
  • 泊松比：材料受拉伸或压缩力时，材料会发生变形，而其横向应变与纵向应变的比值，是一无因次量的物理量。。

塑性​

  • 粘聚力：该值控制屈服面的大小。
  • 内摩擦角：该值控制屈服面的形状。
  • 硬化参数: 该值控制屈服面大小的变化规律，当设置为0时，材料为理想塑性。
  • 剪胀角: 控制塑性势面的形状，当与内摩擦角一致时，则塑性流动为相关联的流动法则。

渗流​

  • 渗透系数（X方向）
  • 渗透系数（Y方向）
  • 孔隙率
  • 压缩系数
  • 水容重